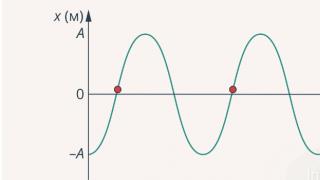
Una funzione f ottenuta dalle funzioni f 1 , f 2 ,…f n utilizzando le operazioni di sostituzione e ridenominazione degli argomenti è detta sovrapposizione funzioni.
Qualsiasi formula che esprime una funzione f come sovrapposizione di altre funzioni specifica un metodo per il suo calcolo, ovvero la formula può essere calcolata se si calcolano i valori di tutte le sue sottoformule. Il valore di una sottoformula può essere calcolato da un insieme noto di valori di variabili binarie.
Utilizzando ciascuna formula, puoi ripristinare la tabella di una funzione logica, ma non viceversa, perché Ogni funzione logica può essere rappresentata da più formule in basi diverse
Vengono chiamate le formule Fi e F j che rappresentano la stessa funzione logica fi equivalente . Quindi le formule equivalenti sono:
1. f 2 (x 1 ; x 2)=(x 1 ×`x 2)=ù(`x 1 Úx 2)= ù(x 1 ®x 2);
2. f 6 (x 1 ; x 2)=(`x 1 ×x 2 Úx 1 ×`x 2)= ù(x 1 “x 2)=(x 1 Åx 2);
3. f 8 (x 1 ; x 2)=(`x 1 ×`x 2)= ù(x 1 Úx 2)=(x 1 ¯x 2);
4. f 14 (x 1 ;x 2)=(`x 1 Ú`x 2)= ù(x 1 ×x 2)=x 1 ½x 2 ;
5. f 9 (x 1 ;x 2)=((`x 1 ×`x 2)Ú(x 1 ×x 2))=(x 1 “x 2) ;
6. f 13 (x 1 ;x 2)= (`x 1 Úx 2)=(x 1 ®x 2).
Se una formula F contiene una sottoformula F i , la sostituzione di F i con una equivalente F j non cambia il valore della formula F per qualsiasi insieme di vettori booleani, ma cambia la forma della sua descrizione. La formula F` appena ottenuta è equivalente alla formula F.
Per semplificare espressioni algebriche complesse, vengono eseguite funzioni booleane trasformazioni equivalenti utilizzando le leggi dell'algebra booleana e regole di sostituzione E sostituzione ,
Quando scrivi formule di algebra booleana, ricorda:
· il numero delle parentesi chiuse è uguale al numero delle parentesi chiuse,
· non ci sono due connettivi logici adiacenti, cioè tra loro deve esserci una formula,
· non ci sono due formule adiacenti, cioè deve esserci una connessione logica tra loro,
· il connettivo logico “×” è più forte del connettivo logico “Ú”,
· se “ù” si riferisce alla formula (F 1 ×F 2) oppure (F 1 Ú F 2), allora occorre innanzitutto eseguire queste trasformazioni secondo la legge di De Morgan: ù(F 1 ×F 2) = ` F 1 Ú` F 2 oppure ù(F 1 ÚF 2)=`F 1 ×`F 2 ;
· operazione " × ” è più forte di “Ú”, che consente di omettere le parentesi.
Esempio: eseguire trasformazioni equivalenti della formula F=x 1 ×x 2 ×x 3 ×`x 4 Ú`x 1 ×x 3 Ú`x 2 ×x 3 Úx 3 ×x 4 .
· secondo la legge della commutatività:
F=x 3 ×x 1 ×x 2 ×`x 4 Úx 3 ×`x 1 Úx 3 ×`x 2 Úx 3 ×x 4 ;
· secondo la legge della distributività:
F=x 3 ×x 1 ×x 2 ×`x 4 Úx 3 ×`x 1 Úx 3 ×(`x 2 Úx 4);
· secondo la legge della distributività:
F=x 3 ×x 1 ×x 2 ×`x 4 Úx 3 ×(`x 1 Ú`x 2 Úx 4);
· secondo la legge della distributività:
F=x 3 ×((x 1 ×x 2 ×`x 4)Ú(`x 1 Ú`x 2 Úx 4));
· secondo la legge di De Morgan:
F=x 3 ×((x 1 ×x 2 ×`x 4)Úù(x 1 ×x 2 ×`x 4));
· secondo la legge di contraddizione:
Quindi x 1 ×x 2 ×x 3 ×`x 4 Ú`x 1 ×x 3 Ú`x 2 ×x 3 Úx 3 ×x 4 =x 3 .
Esempio: eseguire trasformazioni di formule
F=(x 1 ×`x 2 Ú`x 1 ×x 2)×ù(x 1 ×x 2)Ú(x 1 ×x 2)×ù(x 1 ×`x 2 Ú`x 1 ×x 2 );
· secondo la legge di De Morgan
F=(x 1 ×`x 2 Ú`x 1 ×x 2)×(`x 1 Ú`x 2)Ú(x 1 ×x 2)×(`x 1 Úx 2)×(x 1 Ú`x 2);
· secondo la legge della distributività:
F=x 1 ×`x 2 Ú`x 1 ×x 2 Úx 1 ×x 2 ;
· secondo le leggi della commutatività e della distributività:
F= `x 1 ×x 2 Úx 1 ×(`x 2 Úx 2);
· secondo la legge di contraddizione:
F= `x 1 ×x 2 Úx 1 ;
· secondo la legge di Poretsky
Pertanto (x 1 ×`x 2 Ú`x 1 ×x 2)×ù(x 1 ×x 2)Ú(x 1 ×x 2)×ù(x 1 ×`x 2 Ú`x 1 ×x 2 ) = (x2Úx1).
Esempio: trasformare la formula F=ù(`x 1 Úx 2)Ú((`x 1 Úx 3)×x 2).
· secondo la legge di De Morgan:
F= ù(`x 1 Úx 2)×ù((`x 1 Úx 3)×x 2);
· secondo la legge di De Morgan:
F=x 1 ×`x 2 ×(ù(`x 1 Úx 3)Ú`x 2);
· secondo la legge di De Morgan:
F=x 1 ×`x 2 ×(x 1 ×`x 3 Ú`x 2);
· secondo la legge della distributività:
F=x 1 ×`x 2 ×`x 3 Úx 1 ×`x 2 ;
· secondo la legge dell'assorbimento:
Pertanto ù(`x 1 Úx 2)×((`x 1 Úx 3)×x 2)= x 1 ×`x 2 .
Esempio: Converti la formula:
F=ù(x 1 ®x 2)×(`x 3 Ú`x 4)Ú(x 1 ¯x 2)×ù(x 3 ×x 4).
1) trasformare la formula in una base dell'algebra booleana:
F=ù(`x 1 Úx 2)×(`x 3 Ú`x 4)Úù(x 1 Úx 2)× ù(x 3 ×x 4);
2) omettere il segno “`” prima delle variabili binarie:
F=(x 1 ×`x 2)×(`x 3 Ú`x 4)Ú(`x 1 ×`x 2)×(`x 3 Ú`x 4);
3) trasformare la formula secondo la legge distributiva:
F=x 1 ×`x 2 ×`x 3 Úx 1 ×`x 2 ×`x 4 Ú`x 1 ×`x 2 ×`x 3 Ú`x 1 ×`x 2 ×`x 4 ;
4) mettere `x 2 tra parentesi secondo la legge distributiva:
F=`x 2 ×(x 1 ×`x 3 Úx 1 ×`x 4 Ú`x 1 ×`x 3 Ú`x 1 ×`x 4);
5) trasformare secondo la legge della distributività:
F=`x 2 ×(`x 3 ×(x 1 Ú`x 1)Ú`x 4 ×(x 1 Ú`x 1));
6) utilizzare la legge di contraddizione:
F=`x 2 ×(`x 3 Ú`x 4)
Proprietà delle funzioni booleane
Spesso sorge la domanda: ogni funzione booleana è rappresentabile da una sovrapposizione delle formule f 0, f 1,..f 15? Per determinare la possibilità di formare qualsiasi funzione booleana utilizzando una sovrapposizione di queste formule, è necessario determinarne le proprietà e le condizioni per l'utilizzo di un sistema funzionalmente completo.
Funzioni booleane autodualistiche
auto-duale , se f(x 1 ;x 2 ;…x n)=`f(`x 1 ;`x 2 ;…`x n).
Ad esempio, le funzioni f 3 (x 1 ;x 2)=x 1 , f 5 (x 1 ;x 2)=x 2 , f 10 (x 1 ;x 2)=`x 2 e f 12 (x 1 ;x 2)=`x 1 sono autoduali, perché quando il valore dell'argomento cambia, cambiano il loro valore.
Qualsiasi funzione ottenuta mediante operazioni di sovrapposizione da funzioni booleane autoduali è essa stessa autoduale. Pertanto, l'insieme delle funzioni booleane autoduali non consente la formazione di funzioni non autoduali.
Funzioni booleane monotone
Viene chiamata la funzione f(x 1 ; x 2 ;…x n). monotono , se per ogni vettore booleano s 1i £s 2i (s 11 ; s 12 ;……;s 1n) e (s 21 ;s 22 ;……;s 2n) è soddisfatta la seguente condizione: f(s 11 ;s 12 ;… ;s 1i ;…;s 1n)£f(s 21 ;s 22 ;…;s 2i ;…;s 2n).
Ad esempio, per le funzioni f(x 1 ; x 2) le funzioni monotone sono:
se (0; 0) £ (0; 1), allora f(0; 0) £ f (0; 1),
se (0; 0)£(1; 0), allora f(0; 0)£f(1; 0),
se (0; 1)£(1; 1), allora f(0; 1)£f(1; 1),
se (1; 0) £ (1; 1), allora f(1; 0) £ f(1; 1).
Le seguenti funzioni soddisfano queste condizioni:
f0(x1;x2)=0; f1(x1;x2)=(x1×x2); f3(x1; x2)=x1; f5(x1;x2)=x2; f7(x1;x2)=(x1Úx2); f15 (x1; x2)=1.
Qualsiasi funzione ottenuta utilizzando l'operazione di sovrapposizione di funzioni booleane monotone è essa stessa monotona. Pertanto l'insieme delle funzioni monotone non consente la formazione di funzioni non monotone.
Funzioni booleane lineari
L'algebra di Zhegalkin, basata sulla base F 4 =(×; Å; 1), consente di rappresentare qualsiasi funzione logica mediante un polinomio, ciascun termine del quale è una congiunzione di I variabili booleane di un vettore booleano entro 0£i£ N:
P(x 1 ; x 2 ;…x n)=b 0 ×1 Å b i ×x i Å 1 £ j ¹ k £ n b j ×x j ×x k Å……Å b 2n-1 ×x 1 ×x 2 ×... ×xn.
Ad esempio, per le funzioni logiche f 8 (x 1 ; x 2)
Il polinomio di Zhegalkin ha la forma: P(x 1; x 2)=1Å x 1 Å x 2 Å x 1 ×x 2.
I vantaggi dell'algebra di Zhegalkin sono l'aritmetizzazione delle formule logiche, mentre gli svantaggi sono la complessità, soprattutto con un gran numero di variabili binarie.
Polinomi di Zhegalkin che non contengono congiunzioni di variabili binarie, cioè P(x 1 ; x 2 ;…;x n)=b 0 ×1Åb 1 ×x 1 Å…Åb n ×x n si dice lineare .
Ad esempio, f 9 (x 1 ; x 2) = 1Åx 1 Åx 2 , oppure f 12 (x 1 ; x 2) = 1Åx 1 .
Le principali proprietà dell'operazione di addizione modulo 2 sono riportate nella Tabella 1.18.
Se una funzione logica è specificata da una tabella o formula in qualsiasi base, ad es. Se conosci i valori di una funzione booleana per vari insiemi di variabili booleane, puoi calcolarli tutti
coefficienti bi del polinomio di Zhegalkin, compilando un sistema di equazioni per tutti gli insiemi conosciuti di variabili binarie.
Esempio: data una funzione booleana f(x 1 ;x 2)=x 1 Úx 2. I valori di questa funzione sono noti per tutti gli insiemi di variabili booleane.
F(0;0)=0=b 0 ×1Å b 1 ×0 Å b 2 ×0 Å b 3 ×0×0;
f(1;0)=1=b 0 ×1Å b 1 ×1Å b 2 ×0Å b 3 ×1×0;
f(1;1)=1=b 0 ×1Å b 1 ×1Å b 2 ×1Å b 3 ×1×1;
Dove troviamo b 0 =0; b1=1; b2=1; b3 =1.
Pertanto, (x 1 Úx 2)=x 1 Åx 2 Åx 1 ×x 2, cioè la disgiunzione è una funzione booleana non lineare.
Esempio: data una funzione booleana f(x 1 ;x 2)=(x 1 ®x 2). I valori di questa funzione sono noti anche per tutti gli insiemi di variabili binarie.
F(0;0)=1=b 0 ×1Å b 1 ×0 Å b 2 ×0 Å b 3 ×0×0;
f(0;1)=1=b 0 ×1Å b 1 ×0 Å b 2 ×1Å b 3 ×0×1;
f(1;0)=0=b 0 ×1Åb 1 ×1Åb 2 ×0Åb 3 ×1×0;
f(1;1)=1=b 0 ×1Åb 1 ×1Åb 2 ×1Åb 3 ×1×1;
Dove troviamo b 0 =1; b1=1; b2 =0; b3 =1.
Pertanto, (x 1 ®x 2)=1Å x 2 Å x 1 ×x 2.
La Tabella 1.19 mostra i polinomi di Zhegalkin per i principali rappresentanti delle funzioni booleane della Tabella 1.15.
Se viene data un'espressione analitica per una funzione logica e i suoi valori sono sconosciuti per vari insiemi di variabili binarie, allora è possibile costruire un polinomio di Zhegalkin basato sulla base congiuntiva dell'algebra di Boole F 2 =(` ; ×) :
Sia f(x 1 ; x 2)=(x 1 Úx 2).
Allora (x 1 Úx 2)=ù(`x 1 ×`x 2)=((x 1 Å 1)×(x 2 Å 1))Å 1=x 1 ×x 2 Å x 1 ×1Å x 2 × 1Å1×1Å1=
(x 1 Åx 2 Åx 1 ×x 2).
Sia f(x 1 ;x 2)=(x 1 ®x 2).
Allora (x 1 ®x 2)=(`x 1 Úx 2)=ù(x 1 ×`x 2)=x 1 ×(x 2 Å 1)Å 1=x 1 ×x 2 Å x 1 ×1Å 1 = =(1Åx 1 Åx 1 ×x 2).
Sia f(x 1 ;x 2)=(x 1 “x 2).
Allora (x 1 “x 2)=(`x 1 ×`x 2 Úx 1 ×x 2)=ù(ù(`x 1 ×`x 2)×ù(x 1 ×x 2))=((( x 1 Å1)×(x 2 Å1))Å1)× ×(x 1 ×x 2 Å)Å1=(x 1 ×x 2 Åx 1 Åx 2 Å1Å1)×(x 1 ×x 2 Å1)Å1=x 1 ×x 2 Åx 1 ×x 2 Åx 1 ×x 2 Åx 1 Å
x1×x2Åx2Å1=(1Åx1Åx2).
Qualsiasi funzione ottenuta utilizzando l'operazione di sovrapposizione da funzioni logiche lineari è essa stessa lineare. Pertanto l'insieme delle funzioni lineari non consente la formazione di funzioni non lineari.
1.5.6.4. Funzioni che memorizzano "0"
La funzione f(x 1 ; x 2 ;...x n) si dice preservando “0” se per insiemi di valori di variabili binarie (0; 0;...0) la funzione assume il valore f(0; 0;…0)=0 .
Ad esempio, f 0 (0; 0)=0, f 3 (0; 0)=0, f 7 (0; 0)=0, ecc.
Qualsiasi funzione ottenuta utilizzando l'operazione di sovrapposizione da funzioni che preservano "0" è essa stessa una funzione che preserva "0". Pertanto, l'insieme di funzioni che preservano "0" non consente la formazione di funzioni che non preservano "0".
1.5.6.5. Funzioni che memorizzano “1”
La funzione f(x 1 ; x 2 ;…x n) si dice preservando “1” se per insiemi di valori di variabili binarie (1; 1;…1) la funzione assume il valore f(1;1;…1 )=1.
Ad esempio, f 1 (1; 1)=1, f3(1; 1)=1, f 5 (1; 1)=1, ecc.
Qualsiasi funzione ottenuta utilizzando l'operazione di sovrapposizione da funzioni che preservano "1" preserva essa stessa "1". Pertanto l'insieme delle funzioni che preservano “1” non consente la formazione di funzioni che non preservano “1”.
Corrispondenza G tra insiemi UN E IN chiamato sottoinsieme. Se , allora dicono così B
corrisponde UN. L'insieme di tutti gli elementi corrispondenti
Chiamato modo elemento a. Viene chiamato l'insieme di tutti a cui corrisponde l'elemento
prototipo elemento B.
Molte coppie (b, a) tale che si dice inverso
in direzione G ed è designato . I concetti di immagine e prototipo per
"G e sono reciprocamente inversi.
Esempi. 1) Abbiniamolo ad un numero naturale P
insieme di numeri reali 
. Immagine del numero 5
ci sarà un mezzo intervallo
(questo significa il numero intero più grande, minore o uguale a X). Il prototipo del numero 5 in questa corrispondenza è un insieme infinito: semiintervallo.
In termini di chiusura possiamo dare altre definizioni di chiusura e completezza (equivalenti a quelle originali):
K è una classe chiusa se K = [K];
K è un sistema completo se [K] = P 2 .
Esempi.
* (0), (1) - classi chiuse.
* Un insieme di funzioni di una variabile è una classe chiusa.
* - classe chiusa.
* La classe (1, x+y) non è una classe chiusa.
Diamo un'occhiata ad alcune delle classi chiuse più importanti.
1. T0- classe di funzioni che preservano 0.
Indichiamo con T 0 la classe di tutte le funzioni dell'algebra della logica f(x 1 , x 2 , ... , x n) preservando la costante 0, cioè le funzioni per le quali f(0, ... , 0 ) = 0.
È facile vedere che ci sono funzioni che appartengono a T 0 e funzioni che non appartengono a questa classe:
0, x, xy, xÚy, x+y О T 0 ;
Dal fatto che Ï T 0 segue, ad esempio, che non può essere espresso mediante disgiunzione e congiunzione.
Poiché la tabella per la funzione f della classe T 0 contiene il valore 0 nella prima riga, per le funzioni di T 0 è possibile impostare valori arbitrari solo su 2 n - 1 set di valori variabili, ovvero
,
dove è l'insieme delle funzioni che preservano 0 e dipendono da n variabili.
Mostriamo che T 0 è una classe chiusa. Poiché xÎT 0 , allora per giustificare la chiusura è sufficiente mostrare la chiusura rispetto all'operazione di sovrapposizione, poiché l'operazione di cambiamento di variabili è un caso speciale di sovrapposizione con la funzione x.
Permettere . Allora è sufficiente dimostrarlo. Quest'ultimo segue dalla catena delle uguaglianze
2. T1- classe di funzioni che preservano 1.
Indichiamo con T 1 la classe di tutte le funzioni dell'algebra della logica f(x 1, x 2, ... , x n) preservando la costante 1, cioè le funzioni per le quali f(1, ... , 1 ) = 1.
È facile vedere che ci sono funzioni che appartengono a T 1 e funzioni che non appartengono a questa classe:
1, x, xy, xÚy, xºy О T 1 ;
0, , x+y Ï T 1 .
Dal fatto che x + y Ï T 0 segue, ad esempio, che x + y non può essere espresso in termini di disgiunzione e congiunzione.
I risultati relativi alla classe T 0 vengono banalmente trasferiti alla classe T 1 . Quindi abbiamo:
T 1 - classe chiusa;
.
3.L- classe di funzioni lineari.
Indichiamo con L la classe di tutte le funzioni dell'algebra della logica f(x 1 , x 2 , ... , x n) lineari:
È facile vedere che ci sono funzioni che appartengono a L e funzioni che non appartengono a questa classe:
0, 1, x, x+y, x 1 º x 2 = x 1 + x 2 + 1, = x+1 О L;
Proviamo, ad esempio, che xÚy Ï L .
Supponiamo il contrario. Cercheremo un'espressione per xÚy sotto forma di funzione lineare a coefficienti indeterminati:
Per x = y = 0 abbiamo a=0,
per x = 1, y = 0 abbiamo b = 1,
per x = 0, y = 1 abbiamo g = 1,
ma allora per x = 1, y = 1 abbiamo 1v 1 ¹ 1 + 1, che dimostra la non linearità della funzione xy.
La dimostrazione della chiusura della classe delle funzioni lineari è abbastanza ovvia.
Poiché una funzione lineare è determinata univocamente specificando i valori n+1 del coefficiente a 0 , ... , an , il numero di funzioni lineari nella classe L (n) di funzioni dipendenti da n variabili è pari a 2 n+1 .
.
4.S- classe di funzioni autoduali.
La definizione della classe delle funzioni autoduali si basa sull'utilizzo del cosiddetto principio di dualità e delle funzioni duali.
Viene richiamata la funzione definita dall'uguaglianza duale alla funzione .
Ovviamente la tabella della funzione duale (con l'ordinamento standard degli insiemi di valori variabili) si ottiene dalla tabella della funzione originaria invertendo (cioè sostituendo 0 con 1 e 1 con 0) la colonna dei valori della funzione e girandolo.
È facile vederlo
(x 1Ú x 2)* = x 1Ú x 2 ,
(x 1 Ù x 2)* = x 1 Ù x 2 .
Dalla definizione segue che (f*)* = f, cioè la funzione f è duale di f*.
Lascia che una funzione sia espressa usando la sovrapposizione attraverso altre funzioni. La domanda è: come costruire una formula che implementi ? Indichiamo con = (x 1, ..., x n) tutti i diversi simboli di variabile presenti negli insiemi.
Teorema 2.6. Se la funzione j si ottiene come sovrapposizione delle funzioni f, f 1, f 2, ..., f m, cioè
una funzione duale a una sovrapposizione è una sovrapposizione di funzioni duali.
Prova.
j*(x 1 ,...,x n) = ` f(`x 1 ,...,`x n) =
Il teorema è stato dimostrato. ð
Dal teorema consegue il principio di dualità: se una formula A realizza la funzione f(x 1 , ... , x n), allora la formula ottenuta da A sostituendo le funzioni in essa incluse con le loro duali realizza la funzione duale f *(x1, ..., xn).
Indichiamo con S la classe di tutte le funzioni autoduali di P 2:
S = (f | f* = f )
È facile vedere che ci sono funzioni che appartengono a S e funzioni che non appartengono a questa classe:
0, 1, xy, xÚyÏ S .
Un esempio meno banale di funzione autoduale è la funzione
h(x, y, z) = xyÚxzÚyz;
Usando il teorema sulla funzione duale di sovrapposizione, abbiamo
h*(x, y, z)= (x Ú y)Ù(x Ú z) Ù (y Ù z) = x y Ú x z Ú y z; h = h* ; h О S.
Per una funzione auto-duale, l'identità vale
quindi sui set 
e , che chiameremo opposta, la funzione auto-duale assume valori opposti. Ne consegue che la funzione autoduale è completamente determinata dai suoi valori nella prima metà delle righe della tabella standard. Pertanto, il numero di funzioni autoduali nella classe S (n) di funzioni dipendenti da n variabili è pari a:
.
Dimostriamo ora che la classe S è chiusa. Poiché xÎS , allora per giustificare la chiusura è sufficiente mostrare la chiusura rispetto all'operazione di sovrapposizione, poiché l'operazione di cambiamento di variabili è un caso speciale di sovrapposizione con la funzione x. Permettere . Allora è sufficiente dimostrarlo. Quest'ultimo è installato direttamente:
5.M- classe di funzioni monotone.
Prima di definire il concetto di funzione monotona nell'algebra logica, è necessario introdurre una relazione ordinatrice sull'insieme degli insiemi delle sue variabili.
Dicono che il set viene prima del set 
(o “non più di”, o “minore o uguale a”), e usa la notazione if a i £ b i per tutti i = 1, ... , n. Se e , allora diremo che l'insieme precede strettamente l'insieme (o “strettamente minore”, o “minore di” l'insieme), e utilizzeremo la notazione . Gli insiemi e si dicono comparabili se , oppure . Nel caso in cui nessuna di queste relazioni valga, gli insiemi e si dicono incomparabili. Ad esempio, (0, 1, 0, 1) £ (1, 1, 0, 1), ma gli insiemi (0, 1, 1, 0) e (1, 0, 1, 0) non sono comparabili. Pertanto, la relazione £ (spesso chiamata relazione di precedenza) è un ordine parziale sull'insieme B n. Di seguito sono riportati i diagrammi dei set parzialmente ordinati B 2, B 3 e B 4.
 |
 |
La relazione di ordine parziale introdotta è un concetto estremamente importante che va ben oltre lo scopo del nostro corso.
Ora abbiamo l’opportunità di definire il concetto di funzione monotona.
Viene chiamata la funzione di algebra logica monotono, se per due insiemi qualsiasi e , tale che , vale la disuguaglianza 
. L'insieme di tutte le funzioni monotone dell'algebra della logica è indicato con M, e l'insieme di tutte le funzioni monotone dipendenti da n variabili è indicato con M(n).
È facile vedere che ci sono funzioni che appartengono a M e funzioni che non appartengono a questa classe:
0, 1, x, xy, xÚy О M;
x+y, x®y, xºy Ï M .
Mostriamo che la classe delle funzioni monotone M è una classe chiusa. Poiché xОМ, per giustificare la chiusura è sufficiente mostrare la chiusura rispetto all'operazione di sovrapposizione, poiché l'operazione di cambiamento delle variabili è un caso speciale di sovrapposizione con la funzione x.
Permettere . Allora è sufficiente dimostrarlo.
Sia insiemi di variabili, rispettivamente, funzioni j, f 1 , ... , f m , e l'insieme di variabili della funzione j è costituito da quelle e solo quelle variabili che compaiono nelle funzioni f 1 , ... , f m . Siano e due insiemi di valori della variabile e . Questi insiemi definiscono gli insiemi 
valori variabili 
, tale che 
. A causa della monotonicità delle funzioni f 1 , ... , f m
e a causa della monotonicità della funzione f
Da qui otteniamo
Il numero di funzioni monotone dipendenti da n variabili non è noto con esattezza. Il limite inferiore può essere facilmente ottenuto:
dove - è la parte intera di n/2.
Inoltre risulta essere una stima troppo alta dall'alto:
Affinare queste stime è un compito importante e interessante della ricerca moderna.
Criterio di completezza
Ora siamo in grado di formulare e dimostrare un criterio di completezza (teorema di Post), che determina le condizioni necessarie e sufficienti per la completezza di un sistema di funzioni. Premettiamo alla formulazione e alla dimostrazione del criterio di completezza alcuni lemmi necessari che hanno interesse indipendente.
Lemma 2.7. Lemma sulla funzione non auto-duale.
Se f(x 1 , ... , x n)Ï S , allora da esso si può ottenere una costante sostituendo le funzioni x e `x.
Prova. Poiché fÏS esiste un insieme di valori delle variabili
=(a 1 ,...,a n) tale che
f(`a 1 ,...,`a n) = f(a 1 ,...,a n)
Sostituiamo gli argomenti nella funzione f:
x i è sostituito da 
,
cioè mettiamo e consideriamo la funzione
Abbiamo così ottenuto una costante (anche se non si sa quale sia: 0 o 1). ð
Lemma 2.8. Lemma sulla funzione non monotona.
Se la funzione f(x 1 ,...,x n) è non monotona, f(x 1 ,...,x n) Ï M, allora se ne può ottenere una negazione cambiando le variabili e sostituendo le costanti 0 e 1.
Prova. Poiché f(x 1 ,...,x n) Ï M, allora esistono insiemi di valori delle sue variabili, 
, 
, tale che , e per almeno un valore i, a i< b i . Выполним следующую замену переменных функции f:
x sarò sostituito da 
Dopo tale sostituzione otteniamo una funzione di una variabile j(x), per la quale abbiamo:
Ciò significa che j(x)=`x. Il lemma è dimostrato. ð
Lemma 2.9. Lemma sulla funzione non lineare.
Se f(x 1 ,...,x n) Ï L , allora da esso sostituendo le costanti 0, 1 e utilizzando la funzione `x possiamo ottenere la funzione x 1 &x 2 .
Prova. Rappresentiamo f come un DNF (ad esempio, un DNF perfetto) e utilizziamo le relazioni:
Esempio. Diamo due esempi dell'applicazione di queste trasformazioni.
Pertanto, una funzione scritta in forma normale disgiuntiva, dopo aver applicato le relazioni indicate, aprendo parentesi e semplici trasformazioni algebriche, diventa un polinomio mod 2 (polinomio di Zhegalkin):
dove A 0 è una costante e A i è una congiunzione di alcune variabili del numero x 1,..., x n, i = 1, 2, ..., r.
Se ogni congiunzione A i consiste di una sola variabile, allora f è una funzione lineare, il che contraddice la condizione del lemma.
Di conseguenza, nel polinomio di Zhegalkin per la funzione f c'è un termine che contiene almeno due fattori. Senza perdita di generalità, possiamo assumere che tra questi fattori vi siano le variabili x 1 e x 2. Quindi il polinomio può essere trasformato come segue:
f = x 1 x 2 f 1 (x 3 ,..., x n) + x 1 f 2 (x 3 ,..., x n) + x 2 f 3 (x 3 ,..., x n) + f 4 (x3,...,xn),
dove f 1 (x 3 ,..., x n) ¹ 0 (altrimenti il polinomio non comprende una congiunzione contenente la congiunzione x 1 x 2).
Sia (a 3 ,...,a n) tale che f 1 (a 3 ,...,a n) = 1. Allora
j(x 1 ,x 2) = f(x 1 ,x 2 , a 3 ,...,a n) = x 1 x 2 +ax 1 +bx 2 +g ,
dove a, b, g sono costanti uguali a 0 o 1.
Usiamo l'operazione di negazione che abbiamo e consideriamo la funzione y(x 1 ,x 2) ottenuta da j(x 1 ,x 2) come segue:
y(x 1 ,x 2) = j(x 1 +b, x 2 +a)+ab+g.
E' ovvio
y(x 1 ,x 2) =(x 1 +b)(x 2 +a)+a(x 1 +b)+b(x 2 +a)+g+ab+g = x 1 x 2.
Quindi,
y(x1,x2) = x1x2.
Il lemma è completamente dimostrato. ð
Lemma 2.10. Il lemma principale del criterio di completezza.
Se la classe F=( f ) di funzioni dell'algebra della logica contiene funzioni che non preservano l'unità, non conservano 0, sono non autoduali e non monotone:
quindi dalle funzioni di questo sistema, mediante operazioni di sovrapposizione e sostituzione di variabili, si ottengono le costanti 0, 1 e la funzione.
Prova. Consideriamo la funzione. Poi
.
Ci sono due possibili casi di considerazioni successive, designati nella seguente presentazione come 1) e 2).
1). La funzione sull'unità impostata assume il valore 0:
.
Sostituiamo tutte le variabili della funzione con la variabile x. Quindi la funzione
c'è, perché
E 
.
Prendiamo una funzione non auto-duale. Poiché abbiamo già ottenuto la funzione, allora con il lemma su una funzione non auto-duale (lemma 2.7. ) puoi ottenere una costante da. La seconda costante può essere ottenuta dalla prima utilizzando la funzione. Quindi, nel primo caso considerato, si ottengono costanti e negazione. . Il secondo caso, e con esso il lemma principale del criterio di completezza, sono completamente dimostrati. ð
Teorema 2.11. Un criterio per la completezza dei sistemi di funzioni nell'algebra della logica (teorema di Post).
Affinché il sistema di funzioni F = (f i) sia completo è necessario e sufficiente che esso non sia interamente contenuto in nessuna delle cinque classi chiuse T 0, T 1, L, S, M, cioè per in ciascuna delle classi T 0 , T 1 , L , S, M in F esiste almeno una funzione che non appartiene a questa classe.
Necessità. Sia F un sistema completo. Supponiamo che F sia contenuta in una delle classi indicate, denotiamola con K, cioè F Í K. L'ultima inclusione è impossibile, poiché K è una classe chiusa che non è un sistema completo.
Adeguatezza. Supponiamo che l'intero sistema di funzioni F = (f i ) non sia contenuto in nessuna delle cinque classi chiuse T 0 , T 1 , L , S , M . Prendiamo le seguenti funzioni in F:
Quindi, in base al lemma principale (lemma 2.10 ) da una funzione che non preserva 0, una funzione che non preserva 1, funzioni non autoduali e non monotone, si ottengono le costanti 0, 1 e la funzione di negazione:
.
In base al lemma sulle funzioni non lineari (lemma 2.9 ) dalle costanti, dalla negazione e da una funzione non lineare si ottiene la congiunzione:
.
Sistema di funzioni 
- un sistema completo secondo il teorema sulla possibilità di rappresentare qualsiasi funzione dell'algebra della logica sotto forma di una forma normale disgiuntiva perfetta (si noti che la disgiunzione può essere espressa attraverso congiunzione e negazione nella forma 
).
Il teorema è completamente dimostrato. ð
Esempi.
1. Mostriamo che la funzione f(x,y) = x|y forma un sistema completo. Costruiamo una tabella dei valori della funzione x½y:
| X | sì | x|y |
f(0,0) = 1, quindi x | sìT 0 .
f(1,1) = 0, quindi x | sì 1 .
f(0,0) = 1, f(1,1) = 0, quindi x | sìM.
f(0,1) = f(1,0) = 1, - su insiemi opposti x | y assume gli stessi valori, quindi x | sì.
Infine, cosa significa la non linearità della funzione?
x| sì.
In base al criterio di completezza possiamo affermare che f(x,y) = x | y forma un sistema completo. ð
2.
Mostriamo che il sistema di funzioni 
costituisce un sistema completo.
Veramente, .
Quindi, tra le funzioni del nostro sistema abbiamo trovato: una funzione che non preserva 0, una funzione che non preserva 1, funzioni non autoduali, non monotone e non lineari. In base al criterio di completezza si può sostenere che il sistema delle funzioni costituisce un sistema completo. ð
Pertanto, siamo convinti che il criterio di completezza fornisca un modo costruttivo ed efficace per determinare la completezza dei sistemi di funzioni nell'algebra della logica.
Formuliamo ora tre corollari dal criterio di completezza.
Corollario 1. Qualsiasi classe chiusa K di funzioni dell'algebra della logica che non coincide con l'intero insieme delle funzioni dell'algebra della logica (K¹P 2) è contenuta in almeno una delle classi chiuse costruite.
Definizione. Si chiama la classe chiusa K pre-completo, se K è incompleta e per qualsiasi funzione fÏ K la classe K È (f) è completa.
Dalla definizione segue che la classe precompleta è chiusa.
Corollario 2. Nell'algebra della logica esistono solo cinque classi precomplete, e cioè: T 0, T 1, L, M, S.
Per dimostrare il corollario basta verificare che nessuna di queste classi sia contenuta nell'altra, il che è confermato, ad esempio, dalla seguente tabella di funzioni appartenenti a classi diverse:
| T0 | T1 | l | S | M | |
| + | - | + | - | + | |
| - | + | + | - | + | |
| - | - | + | + | - |
Corollario 3. Da qualsiasi sistema completo di funzioni è possibile distinguere un sottosistema completo contenente non più di quattro funzioni.
Dalla dimostrazione del criterio di completezza segue che non si possono distinguere più di cinque funzioni. Dalla dimostrazione del lemma principale (Lemma 2.10
) ne consegue 
o non è sé-duale oppure non preserva l'unità e non è monotono. Pertanto, non sono necessarie più di quattro funzioni.
Facciamo conoscenza con il concetto di sovrapposizione (o imposizione) di funzioni, che consiste nel sostituire una funzione di un altro argomento invece dell'argomento di una determinata funzione. Ad esempio, una sovrapposizione di funzioni dà una funzione e le funzioni si ottengono in modo simile
In generale, supponiamo che una funzione sia definita in un certo dominio e la funzione sia definita in un dominio e i suoi valori siano tutti contenuti nel dominio, allora la variabile z, come si dice, attraverso y, è essa stessa una funzione di
Dato un dato valore, prima trovano il valore y corrispondente ad esso (secondo la regola caratterizzata da un segno), e poi impostano il corrispondente valore y (secondo la regola
caratterizzato da un segno, il suo valore viene considerato corrispondente alla x selezionata. La funzione risultante da una funzione o da una funzione complessa è il risultato di una sovrapposizione di funzioni
L'ipotesi che i valori della funzione non vadano oltre i limiti della regione Y in cui è definita la funzione è molto significativa: se viene omessa, può risultare un'assurdità. Ad esempio, supponendo di poter considerare solo quei valori di x per i quali altrimenti l'espressione non avrebbe senso.
Riteniamo utile sottolineare qui che la caratterizzazione di una funzione come complessa non è legata alla natura della dipendenza funzionale di z da x, ma solo al modo in cui questa dipendenza è specificata. Ad esempio, lascia y per Then
Qui la funzione si è rivelata specificata come funzione complessa.
Ora che il concetto di sovrapposizione di funzioni è pienamente compreso, possiamo caratterizzare con precisione le più semplici tra quelle classi di funzioni che si studiano in analisi: si tratta innanzitutto delle funzioni elementari sopra elencate e poi di tutte quelle che da esse si ottengono utilizzando quattro operazioni aritmetiche e sovrapposizioni, applicate successivamente un numero finito di volte. Si dice che siano espressi attraverso gli elementari nella loro forma finale; a volte vengono anche chiamati elementari.
Successivamente, avendo padroneggiato un apparato analitico più complesso (serie infinite, integrali), conosceremo altre funzioni che svolgono anche un ruolo importante nell'analisi, ma vanno già oltre la classe delle funzioni elementari.
Argomento: “Funzione: concetto, modalità di assegnazione, caratteristiche principali. Funzione inversa. Sovrapposizione di funzioni."
Epigrafe della lezione:
“Studia qualcosa e non pensarci
imparato - assolutamente inutile.
Pensare a qualcosa senza studiarlo
argomento preliminare di riflessione -
Confucio.
Scopo e obiettivi psicologici e pedagogici della lezione:
1) Obiettivo educativo (normativo) generale: Ripassare con gli studenti la definizione e le proprietà di una funzione. Introdurre il concetto di sovrapposizione di funzioni.
2) Obiettivi dello sviluppo matematico degli studenti: utilizzo di materiale educativo e matematico non standard per continuare lo sviluppo dell'esperienza mentale degli studenti, la struttura cognitiva significativa della loro intelligenza matematica, comprese le capacità di pensiero reversibile logico-deduttivo e induttivo, analitico e sintetico, pensiero algebrico e figurativo-grafico , generalizzazione e concretizzazione significativa, alla riflessione e all'indipendenza come capacità metacognitiva degli studenti; continuare lo sviluppo di una cultura del discorso scritto e orale come meccanismi psicologici dell'intelligenza educativa e matematica.
3) Compiti educativi: proseguire l'educazione personale negli studenti di interesse cognitivo per la matematica, responsabilità, senso del dovere, indipendenza accademica, capacità comunicativa di cooperare con il gruppo, insegnante, compagni di classe; capacità autogogica per attività educative e matematiche competitive, ricercando risultati elevati e più alti (motivo acmeico).
Tipo di lezione: imparare nuovo materiale; secondo il criterio del principale contenuto matematico - una lezione pratica; secondo il criterio del tipo di interazione informativa tra studenti e insegnante - una lezione di cooperazione.
Attrezzatura per le lezioni:
1. Letteratura educativa:
1) Kudryavtsev dell'analisi matematica: libro di testo. per universitari e studenti universitari. In 3 volumi T. 3. – 2a ed., riveduta. e aggiuntivi – M.: Più in alto. scuola, 1989. – 352 pag. : malato.
2) Problemi di Demidovich ed esercizi di analisi matematica. – 9a ed. – M.: Casa editrice “Nauka”, 1977.
2. Illustrazioni.
Durante le lezioni.
1. Annuncio dell'argomento e obiettivo educativo principale della lezione; stimolare il senso del dovere, della responsabilità e dell'interesse cognitivo degli studenti in preparazione alla sessione.
2.Ripetizione di materiale basato su domande.
a) Definire una funzione.
Uno dei concetti matematici di base è il concetto di funzione. Il concetto di funzione è associato alla creazione di una relazione tra elementi di due insiemi.
Siano due insiemi non vuoti e siano dati. Viene chiamata una corrispondenza f che corrisponde a ciascun elemento con uno e un solo elemento funzione e scrive y = f(x). Dicono anche che la funzione f visualizza molti su molti.
https://pandia.ru/text/79/018/images/image003_18.gif" larghezza="63" altezza="27">.gif" larghezza="59" altezza="26"> si chiama insieme di significati funzione f ed è indicata con E(f).
b) Funzioni numeriche. Grafico della funzione. Metodi per specificare le funzioni.
Sia data la funzione.
Se gli elementi degli insiemi e sono numeri reali, viene chiamata la funzione f funzione numerica . Si chiama la variabile x discussione o variabile indipendente, e y – funzione O variabile dipendente(da x). Per quanto riguarda le quantità x e y stesse, si dice che siano presenti dipendenza funzionale.
Grafico della funzione y = f(x) è l'insieme di tutti i punti del piano Oxy, per ciascuno dei quali x è il valore dell'argomento e y è il corrispondente valore della funzione.
Per specificare la funzione y = f(x), è necessario specificare una regola che permetta, conoscendo x, di trovare il corrispondente valore di y.
I tre modi più comuni per specificare una funzione sono: analitico, tabulare e grafico.
Metodo analitico: Una funzione è specificata come una o più formule o equazioni.
Per esempio:
Se il dominio di definizione della funzione y = f(x) non è specificato, allora si assume che coincida con l'insieme di tutti i valori dell'argomento per cui ha senso la formula corrispondente.
Il metodo analitico per specificare una funzione è il più avanzato, poiché include metodi di analisi matematica che consentono di studiare completamente la funzione y = f(x).
Metodo grafico: Imposta il grafico della funzione.
Il vantaggio di un compito grafico è la sua chiarezza, lo svantaggio è la sua imprecisione.
Metodo tabulare: Una funzione è specificata da una tabella di una serie di valori di argomento e valori di funzione corrispondenti. Ad esempio, tabelle ben note di valori di funzioni trigonometriche, tabelle logaritmiche.
c) Principali caratteristiche della funzione.
1. Viene chiamata la funzione y = f(x), definita sull'insieme D Anche , se le condizioni e f(-x) = f(x) sono soddisfatte; strano , se le condizioni e f(-x) = -f(x) sono soddisfatte.
Il grafico di una funzione pari è simmetrico rispetto all'asse Oy, mentre una funzione dispari è simmetrica rispetto all'origine. Ad esempio, – anche funzioni; e y = sinx, https://pandia.ru/text/79/018/images/image014_3.gif" width="73" Height="29"> – funzioni di forma generale, cioè né pari né dispari .
2. Sia definita la funzione y = f(x) sull'insieme D e sia . Se per qualsiasi valore degli argomenti segue la seguente disuguaglianza: 
, quindi viene chiamata la funzione crescente
sul set; Se 
, quindi viene chiamata la funzione non decrescente
su https://pandia.ru/text/79/018/images/image021_1.gif" width="117" Height="28 src=">quindi viene chiamata la funzione. decrescente
SU ; 
- non crescente
.
Funzioni crescenti, non crescenti, decrescenti e non decrescenti sul set https://pandia.ru/text/79/018/images/image023_0.gif" width="13" Height="13">valore D (x +T)D e vale l'uguaglianza f(x+T) = f(x).
Per tracciare il grafico di una funzione periodica di periodo T, è sufficiente tracciarlo su un segmento qualsiasi di lunghezza T e continuarlo periodicamente per tutto il dominio di definizione.
Notiamo le principali proprietà di una funzione periodica.
1) La somma algebrica di funzioni periodiche aventi lo stesso periodo T è una funzione periodica con periodo T.
2) Se la funzione f(x) ha periodo T, allora la funzione f(ax) ha periodo T/a.
d) Funzione inversa.
Sia data una funzione y = f(x) con un dominio di definizione D e un insieme di valori E..gif" width="48" Height="22">, allora una funzione x = z(y) con un dominio di definizione E e un insieme di valori D è definito. Tale funzione viene chiamata z(y). inversione
alla funzione f(x) e si scrive nella seguente forma: 
. Le funzioni y = f(x) e x = z(y) si dicono reciprocamente inverse. Per trovare la funzione x = z(y), inversa alla funzione y = f(x), è sufficiente risolvere l'equazione f(x) = y per x.
Esempi:
1. Per la funzione y = 2x la funzione inversa è la funzione x = ½ y;
2. Per funzione 
la funzione inversa è la funzione .
Dalla definizione di funzione inversa segue che la funzione y = f(x) è inversa se e solo se f(x) specifica una corrispondenza biunivoca tra gli insiemi D ed E. Ne consegue che qualsiasi una funzione strettamente monotona ha un inverso . Inoltre, se una funzione aumenta (diminuisce), allora anche la funzione inversa aumenta (diminuisce).
3. Studio di nuovo materiale.
Funzione complessa.
Sia definita la funzione y = f(u) sull'insieme D, e la funzione u = z(x) sull'insieme, e per il valore corrispondente 
. Allora sull'insieme è definita la funzione u = f(z(x)), che viene chiamata funzione complessa
da x (o sovrapposizione
funzioni specificate, o funzione da funzione
).
Viene chiamata la variabile u = z(x). argomento intermedio funzione complessa.
Ad esempio, la funzione y = sin2x è una sovrapposizione di due funzioni y = sinu eu = 2x. Una funzione complessa può avere diversi argomenti intermedi.
4. Risolvere diversi esempi alla lavagna.
5. Conclusione della lezione.
1) risultati teorici e applicativi della lezione pratica; valutazione differenziata del livello di esperienza mentale degli studenti; il loro livello di padronanza dell'argomento, competenza, qualità del discorso matematico orale e scritto; livello di creatività dimostrato; livello di indipendenza e riflessione; livello di iniziativa, interesse cognitivo per i metodi individuali di pensiero matematico; livelli di cooperazione, competizione intellettuale, desiderio di alti livelli di attività educativa e matematica, ecc.;
2) Annuncio dei voti motivati, punti lezione.
